- They are caused by the accelerating movements of the bodies. This is one of the most marvellous natural law. An acceleration is always caused by a force, but Nature always creates a kind of counterforce in order to assure a perfect dynamic equilibrium for all moving bodies, which is called inertia force in Physics.
Remark: In the universe, everything is always moving and accelerating. A perfect constant linear velocity does not exist. Consequently, each body is always affected by some inertia forces. It is said that an inertia-free point does not exist in the universe. Fortunately, we can deal with most of the problems by neglecting the inertia effects caused by the rotation and revolution of the earth or other celestial units.
- The inertia force has an interesting particularity. It affects individually each elementary unit inside the accelerating body. This means that an accelerating force should act individually on each elementary unit. In a rigid body, the elementary units (molecules, atoms) are firmly tied together. The elementary units are accelerating together with the whole body.
- When we are sitting in an accelerating car, the acceleration of our body is assured only if we are tied to the rigid structure of the car. In the case of a frontal collision, and without using a seat belt, the acceleration of our body starts only when we hit the front window. (Let us note that a slowing down should be considered as a negative acceleration.)
- It is a difficult task to specify exactly the elementary units of a body which are individually affected by the inertia forces. We know that a body (living or inanimate) is an agglomeration built up of a huge quantity of atoms. Inside the atomic structure, there is a nucleus (which I call sun of the atom) and several electrons (which I call planetary units).
- If we consider an atom accelerating in the direction
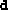 , as shown in Figure 05-01, then each inside unit will be affected by an inertia force in the direction as indicated. The acceleration of an atom must be similar to the acceleration of a vehicle. Each unit inside the atomic structure has its special kind of "seat belt". The law of inertia must be the same for all units of the microcosm.
, as shown in Figure 05-01, then each inside unit will be affected by an inertia force in the direction as indicated. The acceleration of an atom must be similar to the acceleration of a vehicle. Each unit inside the atomic structure has its special kind of "seat belt". The law of inertia must be the same for all units of the microcosm.
- Today, we start to understand that even the members of an atom are complicated structures build up of elementary subatomic particles. So, it is difficult to specify how far we should go in the direction of the infinite little in order to explain the elementary units of an accelerating body. However, to understand the problem, we should imagine a quasi infinite little elementary unit, and we indicate its mass value with the sign
 e. Let us indicate the mass value of the whole body by the sign
e. Let us indicate the mass value of the whole body by the sign  , and the acceleration by
, and the acceleration by  . Then, the inertia force acting on the whole body will be
. Then, the inertia force acting on the whole body will be
 x
x 
It is a resultant vector composed of a huge quantity of elementary inertia forces
 e x
e x 
This resultant force acts in the opposite direction to the acceleration, and passes through the centre of inertia of the accelerating body.
Remark: The centre of inertia is practically the same as the centre of gravity. However, there is a basic difference between inertia and gravity.
- The gravity affects individually each molecule of a body. We should imagine that each molecule is tied to the earth by an invisible elastic string. The resultant of these elementary forces passes through the centre of gravity.
- On the other hand, the elementary units affected by the inertia forces are much smaller than a molecule. The inside of each atom is individually stressed in the case of an acceleration. A human being has a different feeling if he/she strongly accelerates, or he/she is in the outer space without gravitation. A very strong acceleration can even instantaneously kill a living unit. Physicists who try to unify the gravity and the inertia are making a colossal blunder.
- We can consider an average mass value of those elementary units (affected by inertia), and indicate them with the sign |
 e|. Then, we can introduce a quasi infinite big number
e|. Then, we can introduce a quasi infinite big number  , and the inertia force will be
, and the inertia force will be
 x |
x | e| x
e| x  =
=  x
x 
Thus, the value of mass of a body will be
 =
=  x |
x | e|
e|
This means that the value of mass indicates the number of elementary units in the body. In a mass of 2 kilogramme, there are two times as many elementary units as in a mass of 1 kilogramme.
- I already mentioned that some physicists are considering the inertia forces without any reaction, like the other non-newtonian forces. The idea is introduced by observing the inertial phenomenon inside an accelerating system (in the framework of an accelerating coordinate system).
- In a fast running car, if we suddenly apply the brake, then we are thinking that a mysterious force is pushing us forward. Some books are using the expression "apparent force". This name can be misleading. Precisely, we should use the name "apparent" only for such things or for such phenomena which we can directly observe with our vision. A force is not such a thing. Its existence does not depend upon some moving coordinate systems, and we must always find the supporting structure and the reaction force. Meanwhile, sometimes we observe apparent trajectories, and some relative velocities can be apparent, too.
Remark: In modern science, it became a kind of fashion to introduce relative, apparent entities. I would rather like to call this "scientific mania". By considering the speed of light as a universal constant, some scientists introduced the apparent time value, the apparent mass value, and even the apparent energy value. Sometimes, without any reason, those apparent things are considered to be real. This transformation from apparent to real causes a real scientific confusion.
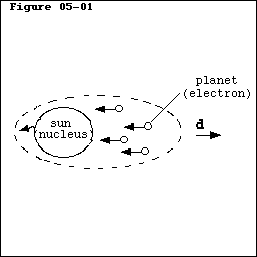
- In Physics, the Coriolis force is introduced with the help of a circular rotating platform, as shown in Figure 05-02 (A).
- It rotates with a constant angular velocity
 . It is assumed that the surface of the platform is perfectly slippery (friction-less). Furthermore, the centre point of the rotation is considered to be inertia-free (neglecting the effects of the rotating earth). A little globe of mass
. It is assumed that the surface of the platform is perfectly slippery (friction-less). Furthermore, the centre point of the rotation is considered to be inertia-free (neglecting the effects of the rotating earth). A little globe of mass  is attached to the centre point with a string of length
is attached to the centre point with a string of length  , and it is following the rotation of the platform. Suddenly, we cut the string and, without a centripetal force, the globe is obliged to change its trajectory. An observer, standing near the platform, will see that the globe moves in a straight line with a velocity
, and it is following the rotation of the platform. Suddenly, we cut the string and, without a centripetal force, the globe is obliged to change its trajectory. An observer, standing near the platform, will see that the globe moves in a straight line with a velocity
 =
=  x
x 
as shown in Figure 05-02 (B). An observer, sitting in the centre point and rotating with the platform, will see that the globe draws a deviated trajectory, as shown in Figure 05-02 (C). He/She attributes this deviation to an apparent force which was introduced as Coriolis force.
- The idea of this apparent Coriolis force is misleading. On a perfectly slippery surface, no horizontal force and reaction force can be created. This is just an apparent trajectory observed by a rotating person.
- Most physicists are obsessed with handling the inertia and the Coriolis problem in reference to an accelerating or rotating coordinate system. Some spectacular mathematical equations have been introduced and, as a result, the following statement was made.
- In a coordinate system, rotating with an angular velocity
 (like our rotating platform), we have to consider two kinds of apparent forces acting on each body (with mass value
(like our rotating platform), we have to consider two kinds of apparent forces acting on each body (with mass value  ).
).
- The so-called centrifugal force. Its value is given by the formula
 ce =
ce =  x
x  x
x  2
2
where  is the distance between the body and the centre of rotation. Its direction is radial, pointing away from the rotation's axis.
is the distance between the body and the centre of rotation. Its direction is radial, pointing away from the rotation's axis.
- If the body moves with a velocity
 on the rotating platform, then we also should consider a Coriolis force, and its value can be calculated by the formula
on the rotating platform, then we also should consider a Coriolis force, and its value can be calculated by the formula
 co = 2 x
co = 2 x  x (
x ( x
x  )
)
where the sign (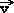 x
x  ) means the vectorial product of the vectors
) means the vectorial product of the vectors  and
and  . The resulting force is perpendicular to both
. The resulting force is perpendicular to both 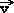 and
and  . If we define the direction of the
. If we define the direction of the  , then we can find the direction of the Coriolis force with the well-known right-hand or left-hand three fingers rule.
, then we can find the direction of the Coriolis force with the well-known right-hand or left-hand three fingers rule.
- According to this formula, the Coriolis force does not depend on the direction of the movement. The only condition is that the velocity vector
 should be on the surface of the rotating platform, which means perpendicular to the rotation's axis. And this is not true. We can prove it with a simple experiment.
should be on the surface of the rotating platform, which means perpendicular to the rotation's axis. And this is not true. We can prove it with a simple experiment.
- Let us consider a large rotating platform on which a person can easily walk or run, as shown in Figure 05-03. Suppose that he/she runs with a velocity
 =
=  x
x 
perpendicular to the radius and in the opposite direction of the rotation as shown. According to the formulae, this person should be affected by a centrifugal force
 ce =
ce =  x
x  x
x  2
2
and a Coriolis force
 co = 2 x
co = 2 x  x
x  x
x  = 2 x
= 2 x  x
x  x
x  2
2
because
 =
=  x
x 
Those two forces are acting in the opposite direction. As a result, we should feel a force
 co -
co -  ce =
ce =  x
x  x
x  2
2
which should push our body in the direction of the rotation's axis. Everybody can find out that this is not true. Anyway, if we examine this situation in a standing (assumed to be inertia-free) system, then it is obvious that the person does not move at all, and no movement means no acceleration and no inertia forces.

- If we start to run in the radial direction, then the situation is different. We feel a force which tries to overturn our body in the right direction (if the direction of the rotation is as indicated in the sketch). We must work harder with our right foot in order to keep our equilibrium.
- We can continue our experiment by running in another direction on the rotating platform. We will still feel this force, but it will always become weaker as we approach the direction perpendicular to the radius. This means that, by evaluating the Coriolis force, only the radial component of the velocity should be considered. In other words, we should consider the speed at which we are approaching the rotating axis or moving from it.
Remark: We should not deviate too much from the radial direction because then the centrifugal force dominates. Anyway, moving perpendicularly to the radius, the Coriolis effect completely disappears.
- This experiment shows that there is a real Coriolis force. Due to the rotation, the trajectory of the moving body is always curved, and this causes a kind of inertia force.
- In order to better understand the problem, it is useful to realise another experiment.
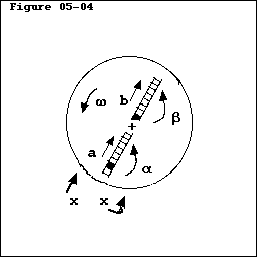
- On a rotating platform, we fix two rails in the radial direction, as shown in Figure 05-04. On each of the rails, there is a kind of vehicle (like a little toy train). Vehicle
 moves towards the rotating axis, and Vehicle
moves towards the rotating axis, and Vehicle  moves away from it. We can draw the trajectories of the vehicles in the standing (inertia-free) system, and we find the curves
moves away from it. We can draw the trajectories of the vehicles in the standing (inertia-free) system, and we find the curves 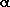 and
and 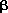 . A curved trajectory means an acceleration, and the vector of this acceleration is pointed towards the centre of curvature.
. A curved trajectory means an acceleration, and the vector of this acceleration is pointed towards the centre of curvature.
- It is interesting to draw a section
 -
- through the vehicle as shown in Figure 05-05.
through the vehicle as shown in Figure 05-05.
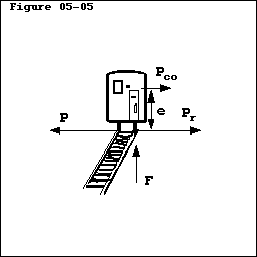
- We can observe four different forces.
- The force
 is causing the acceleration. It obliges the vehicle to follow a curved trajectory. This force is supported by the rail, and the rail must be fixed to the rotating platform. Otherwise, there is no Coriolis acceleration.
is causing the acceleration. It obliges the vehicle to follow a curved trajectory. This force is supported by the rail, and the rail must be fixed to the rotating platform. Otherwise, there is no Coriolis acceleration.
- The force
 r is the reaction force of
r is the reaction force of  . It proves the validity of Newton's third axiom, and it charges the same structure as the force
. It proves the validity of Newton's third axiom, and it charges the same structure as the force  .
.
- The force
 co is a kind of inertia force. It is the result of a quasi infinite number of elementary inertia forces. The resultant force vector passes through the centre of inertia of the vehicle.
co is a kind of inertia force. It is the result of a quasi infinite number of elementary inertia forces. The resultant force vector passes through the centre of inertia of the vehicle.
- Finally, we should mention the force
 . It increases the weight load of the vehicle, and counterbalances the overturning moment
. It increases the weight load of the vehicle, and counterbalances the overturning moment
 co x
co x 
Consequently, there is an additional load on the right wheels of the vehicle (by observing it in the direction of the movement).
Remark: It was observed that, in the northern hemisphere, the right-side wheels and rails are more loaded in places where a train moves in the north-south (or south-north) direction. In the southern hemisphere, the left-side wheels and rails are more loaded. However, the forces caused by the Coriolis effect are weak because of the low angular velocity value of the earth's rotation.
- When a vehicle moves in a circle (circular motion), the picture of the forces is the same as shown in Figure 05-05. This time, the inertia force has a value of
 x
x  x
x  2
2
and it is called centrifugal force. In most of the Physics books, there is a kind of confusion because there is no distinction between the inertia force and the reaction force  r. Our Figure 05-05 shows the important difference between them.
r. Our Figure 05-05 shows the important difference between them.
- We should conclude that the Coriolis force is a kind of inertia force, and as such it is a perfectly newtonian force. This becomes obvious if we consider the elementary inertia forces of an accelerating body. This time, there is no more difference between the force
 co and the force
co and the force  r. It is the reaction force of that force which causes the acceleration. Of course, there must be a supporting structure which ties the elementary unit to the accelerating body. Without this structure, the elementary unit just precipitates until it finds its support. Such a precipitation is sometimes useful in human technology. For a living unit, like a human body, the precipitation of the elementary unit is fatal.
r. It is the reaction force of that force which causes the acceleration. Of course, there must be a supporting structure which ties the elementary unit to the accelerating body. Without this structure, the elementary unit just precipitates until it finds its support. Such a precipitation is sometimes useful in human technology. For a living unit, like a human body, the precipitation of the elementary unit is fatal.
 on a rotating system animated by an angular velocity
on a rotating system animated by an angular velocity  . Since we live on a rotating planet, the Coriolis effect is very common. Nevertheless, the forces are generally weak, and they do not affect our human activities. This is probably the reason why only advanced studies in Physics deal with this phenomenon.
. Since we live on a rotating planet, the Coriolis effect is very common. Nevertheless, the forces are generally weak, and they do not affect our human activities. This is probably the reason why only advanced studies in Physics deal with this phenomenon.
 , as shown in Figure 05-01, then each inside unit will be affected by an inertia force in the direction as indicated. The acceleration of an atom must be similar to the acceleration of a vehicle. Each unit inside the atomic structure has its special kind of "seat belt". The law of inertia must be the same for all units of the microcosm.
, as shown in Figure 05-01, then each inside unit will be affected by an inertia force in the direction as indicated. The acceleration of an atom must be similar to the acceleration of a vehicle. Each unit inside the atomic structure has its special kind of "seat belt". The law of inertia must be the same for all units of the microcosm.

 e. Let us indicate the mass value of the whole body by the sign
e. Let us indicate the mass value of the whole body by the sign  , and the acceleration by
, and the acceleration by  . Then, the inertia force acting on the whole body will be
. Then, the inertia force acting on the whole body will be
 , and the inertia force will be
, and the inertia force will be

 , and it is following the rotation of the platform. Suddenly, we cut the string and, without a centripetal force, the globe is obliged to change its trajectory. An observer, standing near the platform, will see that the globe moves in a straight line with a velocity
, and it is following the rotation of the platform. Suddenly, we cut the string and, without a centripetal force, the globe is obliged to change its trajectory. An observer, standing near the platform, will see that the globe moves in a straight line with a velocity
 ce =
ce =  x
x  )
)

 moves away from it. We can draw the trajectories of the vehicles in the standing (inertia-free) system, and we find the curves
moves away from it. We can draw the trajectories of the vehicles in the standing (inertia-free) system, and we find the curves 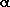 and
and 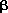 . A curved trajectory means an acceleration, and the vector of this acceleration is pointed towards the centre of curvature.
. A curved trajectory means an acceleration, and the vector of this acceleration is pointed towards the centre of curvature.

 -
-
 . It increases the weight load of the vehicle, and counterbalances the overturning moment
. It increases the weight load of the vehicle, and counterbalances the overturning moment